How to multiply two or three matrices
Matrix multiplication is normally known as dot product of two matrices. There are two types of matrix multiplications.
- Scalar Product
- Vector Product
Matrix Scalar Product
In this method of matrix multiplication a scalar value, that can be said as number constant is multiplied with every value of the entire matrix. This is easy to understand and calculate. In this method we traverse each and every value form entire columns and rows of provided matrix.
Example of Matrix Scalar Product
| Scalar Value | Matrix | Scalar Product | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 |
|
|
Matrix Vector Multiplication
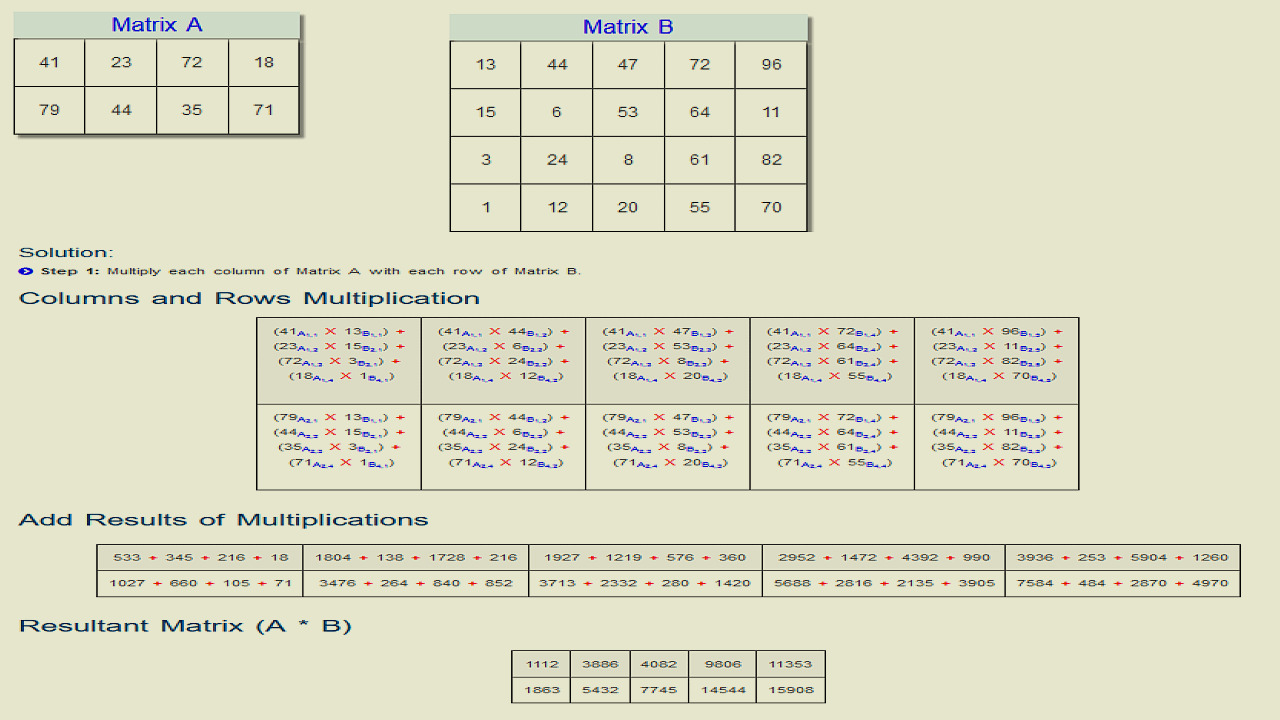
When two vectors/matrices are required to multiply then the elements of these matrices are multiply according to rule. These are two major rules for matrix multiplication.
- The columns of first matrix must be equal to the total rows of second matrix.
- Multiply one after another the columns of first matrix with rows of second column.
- We repeat the above second point for entire columns of first matrix.
- After multiplying each element from column of matrix 1 with matrix 2. We will sum all these product results.
- The resultant matrix (A.B) will have total no of rows equal to the rows in Matrix 1, and it will have total columns equal to the columns in Matrix 2.